even or odd function ,Even and odd functions ,even or odd function,Even and odd functions are named based on the fact that the power function f(x) = x n is an even function, if n is even, and f(x) is an odd function if n is odd. Let us explore other even and odd functions and understand their properties, graphs, . Several Filipinos expressed disbelief after Philippine bet Chelsea Manalo ended her Miss Universe 2024 journey in the Top 30. READ: ‘We never doubted you one bit’: MUPH org congratulates.It was more heartbreaking that it happened with such a very strong representative, Celeste Cortesi. In an exclusive interview with Philstar.com, beauty pageant analyst TIta Lavinia said: “It was the thought at the back of our heads because Celeste is of course one of the frontrunners of this edition. And . Tingnan ang higit pa
0 · How to Tell if a Function is Even, Odd or Neither
1 · Even and Odd Functions
2 · Even and odd functions
3 · How are you supposed to tell even and odd functions
4 · How to Tell if a Function is Even or Odd: Easy Guide
5 · Even and Odd Functions – Properties & Examples
6 · HOW TO TELL IF A FUNCTION IS EVEN OR ODD
Ang konsepto ng "even" (pares) at "odd" (ganap) na function ay mahalaga sa larangan ng matematika, partikular na sa calculus, trigonometry, at complex analysis. Ang pag-unawa sa mga katangian ng mga ganitong uri ng function ay nagbibigay-daan upang pasimplehin ang mga kalkulasyon, lutasin ang mga equation nang mas mabilis, at makakuha ng mas malalim na pag-unawa sa pag-uugali ng iba't ibang mathematical models. Sa artikulong ito, tatalakayin natin nang detalyado kung paano tukuyin kung ang isang function ay even, odd, o neither (wala sa dalawa), kapwa sa pamamagitan ng algebraic at graphical na pamamaraan. Susuriin din natin ang mga kahulugan, magbibigay ng mga halimbawa, at gagamit ng mga diagram at equation upang mas lalong maintindihan ang konsepto.
Ano ang Even Function?
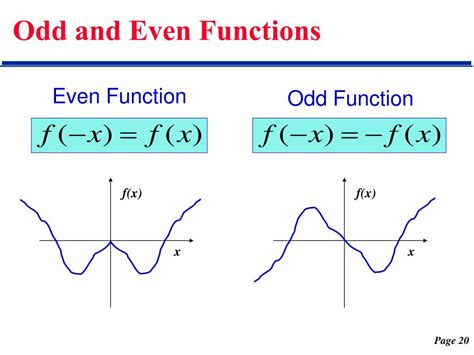
Ang isang function na *f(x)* ay sinasabing "even" kung ito ay sumusunod sa sumusunod na kondisyon:
*f(-x) = f(x)* para sa lahat ng *x* sa domain ng *f*.
Sa madaling salita, kung papalitan natin ang *x* ng *-x* sa equation ng function, at ang resulta ay pareho pa rin sa orihinal na function, kung gayon ang function ay even. Ang graphical na representasyon ng isang even function ay simetriko sa y-axis. Ibig sabihin, kung titingnan mo ang graph sa kaliwa ng y-axis, ito ay eksaktong salamin ng graph sa kanan ng y-axis.
Mga Halimbawa ng Even Functions:
* f(x) = x²: Kung papalitan natin ang *x* ng *-x*, makukuha natin ang *f(-x) = (-x)² = x² = f(x)*. Samakatuwid, ang *f(x) = x²* ay isang even function. Ang graph nito ay isang parabola na nakabukas pataas at simetriko sa y-axis.
* f(x) = cos(x): Ang cosine function ay kilalang even function. *f(-x) = cos(-x) = cos(x) = f(x)*. Ang graph nito ay nagpapakita ng simetriya sa y-axis.
* f(x) = |x|: Ang absolute value function ay isa pang halimbawa. *f(-x) = |-x| = |x| = f(x)*. Ang graph nito ay isang "V" na hugis na simetriko sa y-axis.
* f(x) = x⁴ + 3x² + 5: Kahit na mayroon itong maraming termino, lahat ng mga exponent ng *x* ay even numbers (4 at 2), at ang constant term (5) ay maaari ring ituring na *5x⁰* (kung saan ang 0 ay even). Kung susubukan natin, *f(-x) = (-x)⁴ + 3(-x)² + 5 = x⁴ + 3x² + 5 = f(x)*.
Ano ang Odd Function?
Ang isang function na *f(x)* ay sinasabing "odd" kung ito ay sumusunod sa sumusunod na kondisyon:
*f(-x) = -f(x)* para sa lahat ng *x* sa domain ng *f*.
Ibig sabihin, kung papalitan natin ang *x* ng *-x* sa equation ng function, at ang resulta ay ang negatibo ng orihinal na function, kung gayon ang function ay odd. Ang graphical na representasyon ng isang odd function ay simetriko sa origin. Ibig sabihin, kung i-rotate mo ang graph ng 180 degrees sa paligid ng origin (ang punto (0,0)), makukuha mo pa rin ang parehong graph. Katumbas din ito ng pagsasalamin ng graph sa y-axis at pagkatapos ay sa x-axis.
Mga Halimbawa ng Odd Functions:
* f(x) = x: Kung papalitan natin ang *x* ng *-x*, makukuha natin ang *f(-x) = -x = -f(x)*. Samakatuwid, ang *f(x) = x* ay isang odd function. Ang graph nito ay isang tuwid na linya na dumadaan sa origin at may slope na 1.
* f(x) = sin(x): Ang sine function ay isang kilalang odd function. *f(-x) = sin(-x) = -sin(x) = -f(x)*. Ang graph nito ay nagpapakita ng simetriya sa origin.
* f(x) = x³: Kung papalitan natin ang *x* ng *-x*, makukuha natin ang *f(-x) = (-x)³ = -x³ = -f(x)*.
* f(x) = 5x⁵ - 2x³ + x: Lahat ng mga exponent ng *x* ay odd numbers (5, 3, at 1). *f(-x) = 5(-x)⁵ - 2(-x)³ + (-x) = -5x⁵ + 2x³ - x = -(5x⁵ - 2x³ + x) = -f(x)*.
Paano Tukuyin Kung Ang Isang Function ay Even, Odd, o Neither - Algebraic Method
Ang algebraic method ay ang pinakamabisang paraan upang matukoy kung ang isang function ay even, odd, o neither. Ito ay kinapapalooban ng pagsunod sa mga sumusunod na hakbang:
1. Palitan ang *x* ng *-x* sa equation ng function. Kalkulahin ang *f(-x)*.
2. Pasimplehin ang expression para sa *f(-x)*.
3. Ihambing ang *f(-x)* sa *f(x)*:
* Kung *f(-x) = f(x)*, ang function ay even.
* Kung *f(-x) = -f(x)*, ang function ay odd.
* Kung *f(-x)* ay hindi katumbas ng *f(x)* o *-f(x)*, ang function ay neither even nor odd.
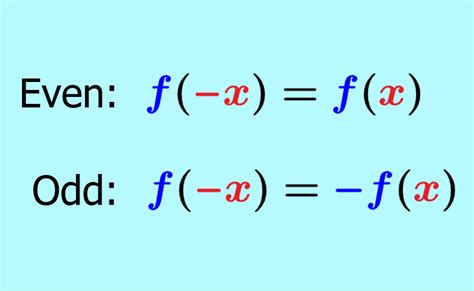
even or odd function Casino Royale had been produced as a 1954 television episode starring Barry Nelson as Bond and Peter Lorre as the villain Le Chiffre, as well as a non-canonical 1967 ensemble satirical film starring David Niven, Peter Sellers and Woody Allen. Eon Productions gained the rights to Casino Royale in 1999 after Sony Pictures Entertainment exchanged them for Metro-Goldwyn-Mayer (MGM.
even or odd function - Even and odd functions